Connecticut eXtreme Croquet Society - "I Didn't Know That!" 3

Featuring eXtreme croquet and eXtreme croquet mallets.

Dedicated to enjoying eXtreme croquet, nature, and the near-death experience!™

Legal

Particle/Wave Duality

By Sam Tudor
Essex, UK

Have you ever noticed that the ball never leaves the hoop in the direction you expect? According to the theory of particle/wave duality, all particles have properties of waves and particles. Thus even a croquet ball has some properties of a wave. The wavelength of a croquet ball is equal to Planck's constant divided by the ball's momentum. As Planck's constant is very small (6.6 x 10-22 MeV), the wavelength of the ball is even smaller. However, when a wave passes through a narrow gap, it diffracts. When the gap is the same width as the wavelength of the wave, the spreading out is complete. Thus, even though the hoop is much wider than the wavelength of the ball, the spreading out is not complete. This wave is not "real" in the sense of a sound wave, but can be imagined as a wave of probability.

Heisenberg's Uncertainty Principle states that the uncertainty in the position multiplied by the uncertainty in the momentum must be equal to or greater than Planck's constant. Thus, you can never know precisely the position and momentum of a particle at the same time. Thus the particle wave allows us to work out the probability of the particle being in a certain place. The same is true with a croquet ball diffracting through a hoop. Once the process is observed, however, the probability wave collapses, as the particle can only be in one place when we observe it.

In fact, if two croquet hoops were positioned next to one another and croquet balls shot at them, providing that the process was not observed by anyone, the waves diffracting out of the two hoops would interfere, producing an unusual distribution of the final resting place of the croquet balls.

Copyright © by Sam Tudor. All rights reserved.

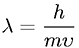
Formula for de Broglie wavelength.

WebMaster